La geometría del tiempo al cruzar la calle

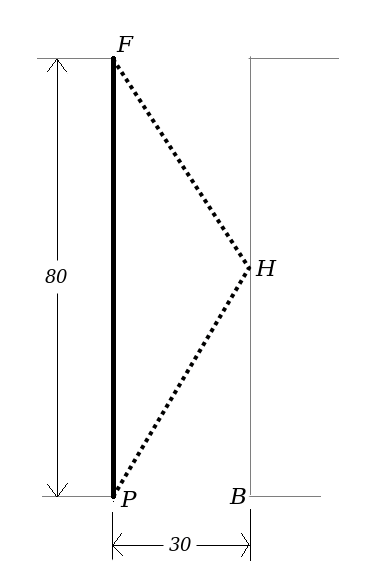
Carlos y Dafne van caminando por la calle. Cuando están en la esquina P, Dafne ve que del otro lado de la calle hay una heladería H. Le pregunta a Carlos si quiere un helado. Carlos le agradece pero no le gustan los helados y contesta negativamente. Carlos continúa caminando en línea recta sobre la banqueta desde P hasta F, mientras que Dafne camina desde P atravesando la calle en diagonal, llega a la heladería H, se compra el helado y vuelve a cruzar la calle en diagonal hasta alcanzar a Carlos en la esquina F. La pregunta es ¿qué distancia caminó Dafne?

De inmediato reconocemos el problema. Es geometría básica, hay que usar el teorema de Pitágoras. Los numeritos de la figura nos dicen que la distancia de P a la heladería H es 50 metros. Lo obtuvimos sumando 30 al cuadrado más 40 al cuadrado y sacamos raíz cuadrada. Por lo tanto, mientras Carlos caminó en línea recta 80 metros, el antojo de Dafne la hizo caminar 100 metros.

Hasta aquí todo es común y corriente. No necesitamos a Einstein para saber cuánto caminaron Carlos y Dafne. Aquí viene el twist de la historia: ¿Qué pasaría si en el teorema de Pitágoras en lugar de sumar el cuadrado de los catetos, los restamos?* Es decir que en lugar de 30^2+40^2 hubiéramos hecho 30^2-40^2. Ahora nos queda un número negativo. Entramos en pánico porque no sabemos qué hacer con una distancia que es la raíz cuadrada de un número negativo.

Como en una película de terror, tocaría salirse del cine o apagar la tele porque lo que acabamos de ver nos ha asustado demasiado. Imaginemos eso, una distancia negativa (o imaginaria en todo caso)... ¿qué cosa podría significar?

Es allí, en contra de todo sentido común, que resulta que ese cálculo raro tiene un significado. Para entenderlo tenemos que cambiar la situación en la que Carlos y Dafne andan caminando. Imaginemos que ahora ambos están en el punto P. Dafne saca un dulce de su bolso y busca donde tirar el envoltorio. Se da cuenta que en la esquina B hay un basurero. Le pide a Carlos que la espere mientras cruza la calle en línea recta de P a B, tira la basura y regresa a la esquina P. Digamos que cruzar la calle de ida y vuelta le tomó 80 segundos**.

La diferencia es que en esta nueva situación, el movimiento ya no ocurre a lo largo y ancho de la calle sino que sólo a lo ancho. Ahora Dafne se atraviesa la calle, camina 60 metros y Carlos no camina nada. Sin embargo ---y esto es lo más hermoso--- podemos seguir usando la misma figura, pero ahora la distancia vertical la usaremos para la dimensión del tiempo, ya no es la longitud de la calle, ya no son 80 metros sino (convenientemente) 80 segundos en el tiempo. Con esto le damos al tiempo la misma categoría que le damos al espacio, es decir, lo interpretamos como una dimensión en donde podemos medir lapsos (distancias) de tiempo. El precio que hay que pagar para que sea consistente es que las distancias a lo largo de la dimensión del tiempo tienen que ser números negativos. Aunque Carlos no se haya movido en espacio, su cuerpo traza un trayectoria recta; y Dafne, al cruzar la calle de P a B y de regreso, traza la trayectoria marcada por la línea punteada. Las líneas de la figura representan ahora trayectorias en el espaciotiempo.

En la geometría espaciotemporal pueden haber distancias positivas, negativas e incluso cero. Una distancia negativa entre dos puntos corresponde al tiempo que transcurre en un reloj que se mueve entre tales puntos. Si la distancia es cero, la interpretamos como la trayectoria de un rayo de luz. Así es la geometría del espaciotiempo. La gravedad surge como una hendidura producida por la presencia de materia en este espacio, ese torcimiento altera la forma de medir distancias, lo cual experimentamos como atracción gravitacional. Un agujero negro viene siendo una región de espaciotiempo altamente curvada.

En esta nueva geometría, Carlos que se quedó siempre en P, medirá en su reloj que a Dafne le toma 80 segundos en ir y venir de P a B, atravesando la calle. Pero el reloj de Dafne marcará 53 segundos, que es la distancia recorrida en el espaciotiempo que resulta de dos veces la raíz cuadrada de 30^2-40^2
(ignorando lo negativo por definición matemática). En el reloj de Dafne el tiempo transcurre más lentamente. Esta es la famosa paradoja de los gemelos. Para la persona que se mueve, el tiempo transcurre más lento que para quien está en reposo.

A través de la historia hemos aprendido que la naturaleza habla el lenguaje de la matemática, mientras más lo estudiemos, más conocemos de nosotros mismos.

Aprovechando el reciente estreno de la película Interstellar, de cuyo elenco también eran parte los agujeros negros, el espacio, el tiempo y la gravedad; no olvidemos que todos ellos son conceptos interconectados a través del lenguaje geométrico del que hemos hablado en los párrafos anteriores. Este es uno de los secretos exquisitos y elegantes de la naturaleza, a veces toman la forma de humildes trazos de yeso en un pizarrón, rindiendo tributo a la imaginación, la exploración y el deseo humano de comprender nuestro lugar en el universo.

_____________

*No hay motivación alguna para cambiar la suma por una resta en el teorema de Pitágoras. Sin embargo es el recurso más simple y dramático de introducir una forma diferente de calcular distancias.

**No usamos aquí los segundos convencionales, sino que los reescalamos para simplificar los cálculos e ilustrar mejor las ideas.